TP 2 : Automates

Ce TP est à effectuer en OCaml, sous Visual Code. Vous pouvez utiliser le Codespace GitHub ou votre ordinateur personnel.
Si vous avez une boucle infinie (le terminal qui ne répond pas) : Ctrl + C

On pourra créer un fichier tp2.ml. Pour exécuter : sélectionner les lignes OCaml et appuyer sur Shift + Entrée. Ceci envoie le code sélectionné dans le terminal (utop). Vous pouvez aussi utiliser utop en mode interactif.
On utilisera ;; à la fin de chaque fonction pour envoyer correctement le code sur utop.

Solution

(* type automate = { 
    initiaux : int list;
    finaux : int list;
    transitions : (int * char * int) list
}

(* 2 *)
let a1 = {
    initiaux = [0];
    finaux = [1];
    transitions = [(0, 'b', 0); (0, 'a', 1); (1, 'a', 0); (1, 'b', 1)]
}
let a2 = {
    initiaux = [0];
    finaux = [2];
    transitions = [(0, 'a', 0); (0, 'b', 1); (1, 'a', 0); (1, 'a', 2); (2, 'b', 2)]
}

(* 3 *)
let miroir a =
  let rec aux = function
      | [] -> []
      | (e, l, e2)::q -> (e2, l, e)::aux q
  in {initiaux = a.finaux; finaux = a.initiaux; transitions = aux a.transitions};;

miroir a1

(* 4 *)
let est_deterministe a =
  let rec aux = function
      | [] -> true
      | (q1, a, q2)::t -> 
          let rec aux2 = function
              | [] -> aux q
              | (q1', a', q2')::t' -> if q1 = q1' && a = a' then false else aux2 t'
          in aux2 q
  in List.length a.initiaux = 1 && aux a.transitions;;

est_deterministe a1;;
est_deterministe a2;; *)

(* 1 *)
type afdc = { 
    initial : int;
    finaux : int list;
    delta : int array array
}
let a1 = {
    initial = 0;
    finaux = [1];
    delta = [|[|1; 0|]; [|0; 1|]|]
}
let a2 = {
    initial = 0;
    finaux = [2];
    delta = [|[|0; 1|]; [|1; 2|]; [|2; 0|]|]
}

(* 2 *)
let rec delta_etoile a q u = match u with
    | [] -> q
    | t::q2 -> delta_etoile a (a.delta.(q).(t)) q2;;

delta_etoile a1 a1.initial [0; 1];;

(* 3 *)
let accepte a u =
  List.mem (delta_etoile a a.initial u) a.finaux;;

accepte a1 [0; 1];;
accepte a1 [1; 0; 0];;

(* 4 *)
let complementaire a =
  let rec aux n = 
    if n = -1 then []
    else if List.mem n a.finaux then aux (n - 1)
    else n::aux (n - 1) in
  {initial = a.initial; finaux = aux (Array.length a.delta - 1); delta = a.delta};;
complementaire a1;;

(* 5 *)
let accessibles a =
  let vus = Array.make (Array.length a.delta) false in
  let rec aux q = 
    vus.(q) <- true;
    for i = 0 to Array.length a.delta.(q) - 1 do
      if not vus.(a.delta.(q).(i)) then aux a.delta.(q).(i)
    done in
  aux a.initial;
  let rec aux2 n = 
    if n = -1 then []
    else if vus.(n) then n::aux2 (n - 1)
    else aux2 (n - 1) in
  aux2 (Array.length a.delta - 1);;
accessibles a1;;

let a3 = {
    initial = 0;
    finaux = [2];
    delta = [|[|1; 0; 0|]; [|0; 1; 0|]; [|1; 0; 2|]|]
};;
accessibles a3;; (* 3 n'est pas accessible *)

(* 6 *)
let vide a =
  List.exists (fun q -> List.mem q a.finaux) (accessibles a);;

(* 7 *)
let inter a b =
  let n = Array.length a.delta in
  let p = Array.length b.delta in
  let s = Array.length a.delta.(0) in
  let d = Array.make_matrix (n*p) s (-1) in
  for i = 0 to n - 1 do
    for j = 0 to p - 1 do
      for k = 0 to s - 1 do
        d.(i*p + j).(k) <- a.delta.(i).(k)*p + b.delta.(j).(k)
      done
    done
  done;
  let rec finaux l1 l2 = match l1, l2 with
    | [], _ -> []
    | _, [] -> []
    | i::q, j::q' -> (i*p + j)::(finaux q l2)@(finaux [i] q') in
  {initial = a.initial*p + b.initial; finaux = finaux a.finaux b.finaux; delta = d};;

let a3 = inter a1 a2;;
accepte a3 [0; 1; 0; 0; 1];;
accepte a3 [0; 1; 1; 0; 0; 1];;
accepte a3 [1; 0; 0; 1];;

(* 8 *)
(* A est inclus dans B ssi A inter (complémentaire de B) est vide *)
let inclus a b =
  vide (inter a (complementaire b));;

(* 9 *)
let equivalent a b =
  inclus a b && inclus b a;;

Automate déterministe

On utilisera le type suivant d'automate déterministe complet (AFDC), où les états sont entre $0$ et $n-1$ et les lettres sont des entiers ($a$ est représenté par $0$, $b$ par $1$...) :

type afdc = { 
    initial : int;
    finaux : int list;
    delta : int array array
}

Si a est de type afdc, a.delta.(i).(j) est l'état atteint en lisant la lettre $j$ à partir de l'état $i$ (c'est-à-dire $\delta(i, j)$). Le nombre d'états de a est donc Array.length a.delta.

1. Définir en OCaml les automates a1 et a2 suivants :

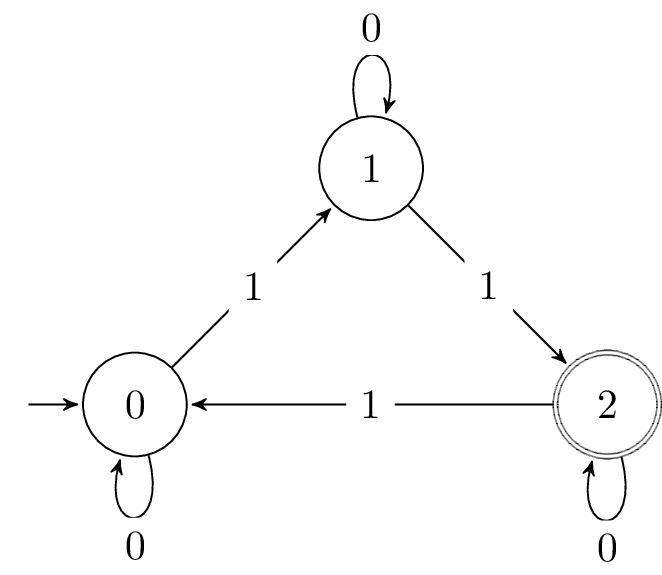
2. Définir une fonction delta_etoile : afdc -> int -> int list -> int telle que delta_etoile a q u renvoie l'état atteint en lisant le mot $u$ à partir de l'état $q$ (c'est-à-dire $\delta^*(q, u)$). Vérifier avec a1.

3. Définir une fonction accepte : afdc -> int list -> bool telle que accepte a u détermine si $u$ est reconnu par a. Vérifier avec a1. Quelle est la complexité de accepte ?

4. Définir une fonction complementaire : afdc -> afdc telle que complementaire a renvoie un automate reconnaissant le complémentaire du langage reconnu par a. Vérifier avec a1.
   Rappel : on a besoin que l'automate soit déterministe complet, ce qui est supposé dans ce TP.

5. Définir une fonction accessibles : afdc -> int list telle que accessibles a renvoie la liste des états accessibles depuis l'état initial de a. Pour cela, on pourra utiliser un parcours en profondeur. Vérifier sur des exemples.

Indice

let accessibles a =
  let vus = ... in (* vus.(i) = true si l'état i a été visité *)
  let rec aux q = (* parcours en profondeur depuis l'état q *)
    ...
  aux a.initial; (* on commence le parcours en profondeur depuis l'état initial *)
  ...

6. En déduire une fonction vide : afdc -> bool déterminant si un automate reconnaît le langage vide.

Automate produit

7. Écrire une fonction inter : afdc -> afdc -> afdc telle que inter a b renvoie un automate reconnaissant l'intersection des langages reconnus par a et b. On suppose que a et b ont le même alphabet.
   Pour cela, on construira l'automate produit de a et b, qui possède $np$ états (où $n$ est le nombre d'états de a et $p$ le nombre d'états de b), et dont l'état $(i, j)$ sera numéroté $i \times p + j$.
   Vérifier avec a1 et a2.

8. En déduire une fonction inclus a b déterminant si le langage reconnu par l'automate a est inclus dans celui reconnu par b. On pourra utiliser les fonctions précédentes.

9. En déduire une fonction equivalent a b déterminant si les langages reconnus par les automates a et b sont égaux.