TP 5 : Algorithme de Kruskal

Solution

#include <stdio.h>
#include <stdlib.h>

typedef struct {
    int u;
    int v;
    int poids;
} arete;

typedef struct {
    int n; // nombre de sommets
    int *degres; // degres[i] = nombre de voisins du sommet i
    arete **aretes; // aretes[i] = tableau des aretes incidentes au sommet i
} graphe;

// 1 
arete a(int u, int v, int poids) {
    arete e;
    e.u = u;
    e.v = v;
    e.poids = poids;
    return e;
}

// 3
int n_aretes(graphe g) {
    int n = 0;
    for (int i = 0; i < g.n; i++) {
        n += g.degres[i];
    }
    return n / 2;
}

// 4
arete* aretes(graphe g) {
    arete* t = malloc(n_aretes(g) * sizeof(arete));
    int k = 0;
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.degres[i]; j++) {
            if (i < g.aretes[i][j].v) {
                t[k] = g.aretes[i][j];
                k++;
            }
        }
    }
    return t;
}


// 5
void tri_insertion(arete* t, int n) {
    for (int i = 1; i < n; i++) {
        arete e = t[i];
        int j = i - 1;
        while (j >= 0 && t[j].poids > e.poids) {
            t[j + 1] = t[j];
            j = j - 1;
        }
        t[j + 1] = e;
    }
}


// 6
typedef struct {
  int n; // nombre d'élements
  int* t; // t[i] = père de i
} uf;
uf* create(int n) {
    uf* u = malloc(sizeof(uf));
    u->n = n;
    u->t = malloc(n * sizeof(int));
    for (int i = 0; i < n; i++) {
        u->t[i] = i;
    }
    return u;
}

// 7
int find(uf* u, int x) {
    if (u->t[x] == x) {
        return x;
    } else {
        return find(u, u->t[x]);
    }
}

// 8
void merge(uf* u, int x, int y) {
    u->t[find(u, x)] = find(u, y);
}

// 9
int n_cc(uf* u) {
    int n = 0;
    for (int i = 0; i < u->n; i++) {
        if (u->t[i] == i) {
            n++;
        }
    }
    return n;
}

// 10
arete* kruskal(graphe g) {
    arete* t = aretes(g);
    tri_insertion(t, n_aretes(g));
    uf* u = create(g.n);
    arete* mst = malloc((g.n - 1) * sizeof(arete));
    int k = 0;
    for (int i = 0; i < n_aretes(g); i++) {
        if (find(u, t[i].u) != find(u, t[i].v)) {
            mst[k] = t[i];
            k++;
            merge(u, t[i].u, t[i].v);
        }
    }
    free(u->t);
    free(u);
    free(t);
    return mst;
}

// 11. Réécrire la fonction `find` pour qu'elle utilise la compression de chemin.  
int find(uf* u, int x) {
    if (u->t[x] == x) {
        return x;
    } else {
        u->t[x] = find(u, u->t[x]);
        return u->t[x];
    }
}

// 12. Redéfinir le type `uf` et réécrire `merge` pour qu'il utilise l'union par rang.
typedef struct {
  int n; // nombre d'élements
  int* t; // t[i] = père de i
  int* h; // h[i] = hauteur de l'arbre enraciné en i
} uf;

void merge(uf* u, int x, int y) {
    int rx = find(u, x);
    int ry = find(u, y);
    if (u->h[rx] < u->h[ry]) {
        u->t[rx] = ry;
    } else if (u->h[rx] > u->h[ry]) {
        u->t[ry] = rx;
    } else {
        u->t[rx] = ry;
        u->h[ry]++;
    }
}

int main() {
    // 2
    graphe g;
    g.n = 7;
    g.degres = malloc(7 * sizeof(int));
    g.degres[0] = 3;
    g.degres[1] = 3;
    g.degres[2] = 4;
    g.degres[3] = 3;
    g.degres[4] = 2;
    g.degres[5] = 3;
    g.degres[6] = 2;
    g.aretes = malloc(10 * sizeof(arete*));
    g.aretes[0] = malloc(3 * sizeof(arete));
    g.aretes[1] = malloc(3 * sizeof(arete));
    g.aretes[2] = malloc(4 * sizeof(arete));
    g.aretes[3] = malloc(3 * sizeof(arete));
    g.aretes[4] = malloc(2 * sizeof(arete));
    g.aretes[5] = malloc(3 * sizeof(arete));
    g.aretes[6] = malloc(2 * sizeof(arete));
    g.aretes[7] = malloc(2 * sizeof(arete));
    g.aretes[8] = malloc(2 * sizeof(arete));
    g.aretes[9] = malloc(2 * sizeof(arete));
    g.aretes[0][0] = g.aretes[1][0] = a(0, 1, 1);
    g.aretes[0][1] = g.aretes[2][0] = a(0, 2, 5);
    g.aretes[0][2] = g.aretes[6][0] = a(0, 6, 5);
    g.aretes[1][1] = g.aretes[3][0] = a(1, 3, 2);
    g.aretes[1][2] = g.aretes[6][1] = a(1, 6, 3);
    g.aretes[2][1] = g.aretes[3][1] = a(2, 3, 3);
    g.aretes[2][2] = g.aretes[4][0] = a(2, 4, 2);
    g.aretes[2][3] = g.aretes[5][0] = a(2, 5, 5);
    g.aretes[3][2] = g.aretes[5][1] = a(3, 5, 1);
    g.aretes[4][1] = g.aretes[5][2] = a(4, 5, 5);

    printf("Nombre d'aretes : %d\n", n_aretes(g));
    arete* t = aretes(g);
    for (int i = 0; i < n_aretes(g); i++) {
        printf("Arete %d : %d %d %d\n", i, t[i].u, t[i].v, t[i].poids);
    }
    arete* mst = kruskal(g);
    for (int i = 0; i < 6; i++) {
        printf("Arete %d : %d %d %d\n", i, mst[i].u, mst[i].v, mst[i].poids);
    }
    // free_graphe(g);
    free(t);
    free(mst);
}

Tri des arêtes

On définit les types suivants pour un graphe pondéré non-orienté en C :

typedef struct {
    int u;
    int v;
    int poids;
} arete;

typedef struct {
    int n; // nombre de sommets
    int *degres; // degres[i] = nombre de voisins du sommet i
    arete **aretes; // aretes[i] = tableau des aretes incidentes au sommet i
} graphe;

0. Écrire une fonction arete a(int u, int v, int poids) renvoyant une nouvelle arête de poids poids entre les sommets u et v.

1. Définir le graphe G1 suivant :

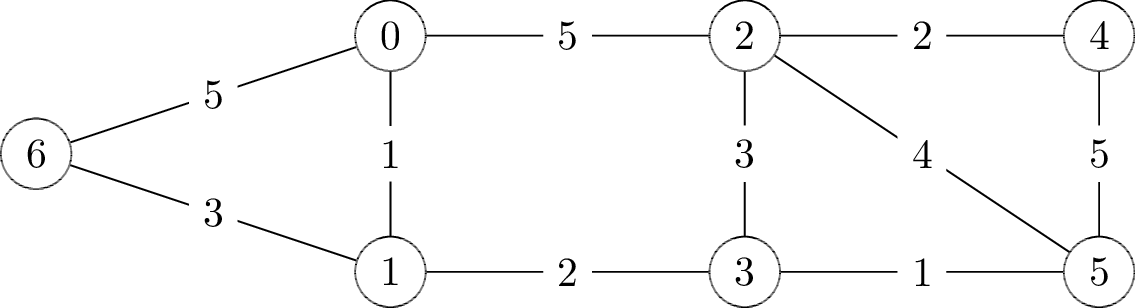
Solution

graphe g;
g.n = 7;
g.degres = malloc(7 * sizeof(int));
g.degres[0] = 3;
g.degres[1] = 3;
g.degres[2] = 4;
g.degres[3] = 3;
g.degres[4] = 2;
g.degres[5] = 3;
g.degres[6] = 2;
g.aretes = malloc(10 * sizeof(arete*));
g.aretes[0] = malloc(3 * sizeof(arete));
g.aretes[1] = malloc(3 * sizeof(arete));
g.aretes[2] = malloc(4 * sizeof(arete));
g.aretes[3] = malloc(3 * sizeof(arete));
g.aretes[4] = malloc(2 * sizeof(arete));
g.aretes[5] = malloc(3 * sizeof(arete));
g.aretes[6] = malloc(2 * sizeof(arete));
g.aretes[0][0] = g.aretes[1][0] = a(0, 1, 1);
g.aretes[0][1] = g.aretes[2][0] = a(0, 2, 5);
g.aretes[0][2] = g.aretes[6][0] = a(0, 6, 5);
g.aretes[1][1] = g.aretes[3][0] = a(1, 3, 2);
g.aretes[1][2] = g.aretes[6][1] = a(1, 6, 3);
g.aretes[2][1] = g.aretes[3][1] = a(2, 3, 3);
g.aretes[2][2] = g.aretes[4][0] = a(2, 4, 2);
g.aretes[2][3] = g.aretes[5][0] = a(2, 5, 5);
g.aretes[3][2] = g.aretes[5][1] = a(3, 5, 1);
g.aretes[4][1] = g.aretes[5][2] = a(4, 5, 5);

2. Écrire une fonction void free_graphe(graphe g) libérant la mémoire allouée pour le graphe g.

On utilisera G1 pour tester les fonctions suivantes.

3. Écrire une fonction int n_aretes(graphe g) renvoyant le nombre d'arêtes du graphe g.
4. Écrire une fonction arete* aretes(graphe g) renvoyant un tableau contenant toutes les arêtes du graphe g.

Le tri par insertion trie un tableau t en parcourant chaque élément t[i] et en le plaçant à sa place dans le sous-tableau trié t[0], t[1], ..., t[i - 1]. Pour le mettre à sa bonne position, on l'échange avec l'élément précédent tant que celui-ci est plus grand.
L'invariant suivant est conservé : à la fin de la $i$-ème itération, le sous-tableau t[0], t[1], ..., t[i] est trié.

5. Écrire une fonction void tri_insertion(arete* aretes, int n) qui trie le tableau aretes de taille n, par poids croissant. Quelle est sa complexité ?

Union-Find

On utilise le type suivant pour représenter une structure Union-Find :

typedef struct {
  int n; // nombre d'élements
  int* t; // t[i] = père de i
} uf;

Si $i$ est une racine, on prendra $t[i] = i$.

6. Écrire une fonction uf create(int n) initialisant une structure Union-Find de taille n.
7. Écrire une fonction int find(uf u, int x) renvoyant la racine de l'arbre contenant x, sans compression de chemin.
8. Écrire une fonction void merge(uf u, int x, int y) fusionnant les arbres contenant x et y, sans optimisation.

Algorithme de Kruskal

9. Écrire une fonction int n_cc(uf u) renvoyant le nombre de composantes connexes de la structure Union-Find u.
10. Écrire une fonction arete* kruskal(graphe g) renvoyant un tableau contenant les arêtes de l'arbre couvrant minimum du graphe g.

Optimisations

11. Réécrire la fonction find pour qu'elle utilise la compression de chemin.
12. Redéfinir le type uf et réécrire merge pour qu'il utilise l'union par rang.

LeetCode

13. Résoudre ce problème LeetCode. Pour cela, il faut utiliser un tri plus rapide que le tri par insertion. Vous pouvez implémenter un tri fusion, en vous inspirant de https://mp2i-info.github.io/7_algo/2_divide_conquer/divide_conquer