TP 7 : Résolution du taquin avec A*

Solution

type state = {
  grid : int array array;
  mutable i : int;
  mutable j : int;
  mutable h : int;
}

let s = { (* exemple de l'énoncé *)
    grid =
        [| [| 2; 3; 1; 6 |];
           [| 14; 5; 8; 4 |];
           [| 15; 12; 7; 9 |];
           [| 10; 13; 11; 0|] |];
    i = 2;
    j = 0;
    h = 34
}
let final = (* l'état dans lequel on doit aboutir *)
  let m = Array.make_matrix 4 4 0 in
  for i = 0 to 3 do
    for j = 0 to 3 do
      m.(i).(j) <- i * 4 + j
    done
  done;
  {grid = m; i = 3; j = 3; h = 0}

type direction = U | D | L | R

let possible_moves s =
  let l = ref [] in
  if s.i < 3 then l := [D];
  if s.i > 0 then l := U::!l;
  if s.j < 3 then l := R::!l;
  if s.j > 0 then l := L::!l;
  !l;;

let compute_h s =
  let h = ref 0 in
  for i = 0 to 3 do
      for j = 0 to 3 do
          let v = s.grid.(i).(j) in
          if v <> 15 then
          h := !h + (abs (i - v/4)) + (abs (j - v mod 4))
      done
  done;
  s.h <- !h;;
compute_h s; s.h;;

let delta_h s d = 
    let (di, dj) = match d with
        | U -> (-1, 0)
        | D -> (1, 0)
        | L -> (0, -1)
        | R -> (0, 1) in
    let i, j = s.i, s.j in
    let v = s.grid.(i + di).(j + dj) in
    (abs (i - v/4)) + (abs (j - v mod 4)) -
    (abs ((i+di) - v/4)) - (abs ((j+dj) - v mod 4))

delta_h s U;;

let apply s d =
    let (di, dj) = match d with
        | U -> (-1, 0)
        | D -> (1, 0)
        | L -> (0, -1)
        | R -> (0, 1) in
    let i, j = s.i, s.j in
    let x = s.grid.(i + di).(j + dj) in
    s.grid.(i + di).(j + dj) <- 15;
    s.grid.(i).(j) <- x;
    s.h <- s.h + delta_h s d;
    s.i <- i + di;
    s.j <- j + dj

apply s U; s;;

let copy s = {
    i = s.i;
    j = s.j;
    h = s.h;
    grid = Array.map (Array.copy) s.grid
}

let successors s =
    let rec aux = function
        | [] -> []
        | d::q -> 
            let s' = copy s in
            apply s' d;
            s'::aux q in
    aux (possible_moves s)

(* penser à réinitialiser s après l'utilisation de apply *)
successors s;;

type 'a abr = V | N of 'a * 'a abr * 'a abr

let rec add a p e = match a with
    | V -> N((p, e), V, V)
    | N(r, g, d) -> if p < fst r then N(r, add g p e, d)
        else  N(r, g, add d p e)
        
let rec extract_min = function
    | V -> failwith "vide"
    | N(r, V, d) -> r, d
    | N(r, g, d) -> 
        let x, g' = extract_min g in
        x, N(r, g', d)

let a_star s =
    let q = ref V in
    q := add !q s.h s;
    let d = Hashtbl.create 42 in
    while not (Hashtbl.mem d final) do
        let (p, e), q' = extract_min !q in
        q := q';
        if not (Hashtbl.mem d e) then (
            let de = p - e.h in
            Hashtbl.replace d e de;
            List.iter (fun s ->
                q := add !q (de + 1 + s.h) s
            ) (successors e)
        )
    done;
    Hashtbl.find d final

let random_state nb_moves =
  let state = copy final in
  for i = 0 to nb_moves - 1 do
    let moves = possible_moves state in
    let n = List.length moves in
    apply state (List.nth moves (Random.int n))
  done;
  state

let ten =
  let moves = [U; U; L; L; U; R; D; D; L; L] in
  let state = copy final in
  List.iter (apply state) moves;
  state

let rs = random_state 10;;
a_star rs;;

let five =   
  {grid = [|[|0; 15; 2; 3|]; [|4; 1; 5; 7|]; [|8; 9; 6; 11|]; [|12; 13; 10; 14|]|];
  i = 0; j = 1; h = -5}

let ten =
  let moves = [U; U; L; L; U; R; D; D; L; L] in
  let state = copy final in
  List.iter (apply state) moves;
  state

a_star five;;
a_star ten;;

Le jeu de taquin est constitué d'une grille $4 \times 4$ dans laquelle sont disposés les entiers de $0$ à $14$ , une case étant laissée libre.
Voici un état initial possible :

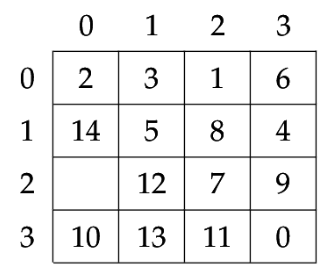
On obtient un nouvel état du jeu en déplaçant dans la case libre le contenu de la case située au-dessus, à gauche, en dessous ou à droite, au choix. Si on déplace par exemple le contenu de la case située à droite de la case libre, c'est-à-dire 12, on obtient le nouvel état suivant :

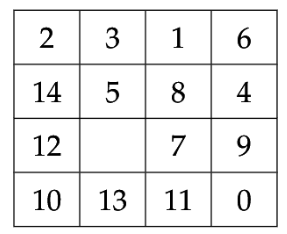
Le but du jeu de taquin est de parvenir à l'état final suivant :

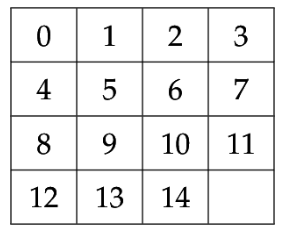
On souhaite résoudre de façon optimale le jeu du taquin, avec une suite de déplacements de longueur minimum permettant de passer d'une configuration initiale à la configuration finale.
Dans le premier exemple ci-dessus, la solution optimale est de longueur 50.

En OCaml, une position sera représentée par le type suivant :

type state = {
  grid : int array array;
  mutable i : int;
  mutable j : int;
  mutable h : int;
}

i et j indique les coordonnées de la case libre (le 15).
grid est une matrice $4 \times 4$ codant la grille. La case libre contiendra toujours la valeur $15$ .
h sera une heuristique estimant la distance de l'état actuel à l'état final, que nous définirons plus loin.

On pourra utiliser les grilles suivantes pour tester :

let s = { (* exemple de l'énoncé *)
    grid =
        [| [| 2; 3; 1; 6 |];
           [| 14; 5; 8; 4 |];
           [| 15; 12; 7; 9 |];
           [| 10; 13; 11; 0|] |];
    i = 2;
    j = 0;
    h = 34
}
let final = (* l'état dans lequel on doit aboutir *)
  let m = Array.make_matrix 4 4 0 in
  for i = 0 to 3 do
    for j = 0 to 3 do
      m.(i).(j) <- i * 4 + j
    done
  done;
  {grid = m; i = 3; j = 3; h = 0}

Graphe du taquin

Une configuration du taquin se code naturellement comme une permutation de $\{0, ..., 15\}$ , où le 15 correspond à la case vide.
On peut alors définir le graphe (non orienté) $G$ du taquin où chaque sommet $s$ de $G$ est une grille et il y a une arête entre $s$ et $s'$ si on peut passer de $s$ à $s'$ en une étape.

Remarque : on peut montrer que $G$ possède exactement deux composantes connexes, contenant chacune la moitié des sommets.

Quel est le nombre de sommets de $G$ ? Le nombre approximatif d'arêtes ? Est-il raisonnable de stocker $G$ explicitement en mémoire ?

On code un déplacement par le type suivant, où U, par exemple, correspond à un déplacement de la case libre vers le haut :

type direction = U | D | L | R

Écrire une fonction possible_moves : state -> direction list qui renvoie la liste des directions de déplacement légales à partir d'un certain état.

possible_moves s;;
- : direction list = [R; U; D]

Pour orienter la recherche, on définit une heuristique $h$ comme suit qui associe à chaque état du taquin un entier positif ou nul. Pour $e$ un état (grille) et $v \in \{0, ..., 14\}$ , on note $e_{v}^{i}$ la ligne de l'entier $v$ dans $e$ et $e_{v}^{j}$ sa colonne. On pose alors :

h(e) = \sum_{v = 0}^{14} | e_v^i - \left\lfloor \frac{v}{4} \right\rfloor | + |e_v^j - (v \textnormal{ mod } 4)|

$h(e)$ est donc la somme, pour chaque valeur $v$ de la grille, de la distance entre sa position actuelle et sa position dans la grille finale.
Plus $h(e)$ est petit, plus la grille semble proche de l'état finale. On peut montrer que $h(e)$ est une borne inférieure de la distance entre $e$ et la grille finale.

Écrire une fonction compute_h : state -> unit qui prend en entrée un état, dans lequel le champ h a une valeur quelconque, et donne à ce champ la bonne valeur.

compute_h s; s.h;;
- : int = 34

Écrire une fonction delta_h : state -> direction -> int qui prend en entrée un état $e$ et une direction $d$ et renvoie la différence $h(e') - h(e)$ , où $e'$ est l'état que l'on atteint à partir de $e$ en effectuant le déplacement $d$ . On ne fera que les calculs nécessaires (on évitera donc de recalculer toute la somme définissant $h$ ).

delta_h s U;;
- : int = -1

Écrire une fonction apply : state -> direction -> unit qui modifie un état en lui appliquant un déplacement, que l'on supposera légal.

apply s U; s;;
- : state =
{grid =
  [|[|2; 3; 1; 6|]; [|15; 5; 8; 4|]; [|14; 12; 7; 9|]; [|10; 13; 11; 0|]|];
 i = 1; j = 0; h = 33}

Écrire une fonction copy : state -> state qui prend un état et en renvoie une copie.
On pourra utiliser la fonction Array.copy, mais attention : grid est un tableau de tableaux...

Algorithme A*

Écrire une fonction successors : state -> state list qui prend en entrée un état et renvoie la liste de ses voisins.

successors s;; (* penser à réinitialiser s après l'utilisation de apply *)
- : state list =
[{grid =
   [|[|2; 3; 1; 6|]; [|14; 5; 8; 4|]; [|12; 15; 7; 9|]; [|10; 13; 11; 0|]|];
  i = 2; j = 1; h = 39};
 {grid =
   [|[|2; 3; 1; 6|]; [|15; 5; 8; 4|]; [|14; 12; 7; 9|]; [|10; 13; 11; 0|]|];
  i = 1; j = 0; h = 37};
 {grid =
   [|[|2; 3; 1; 6|]; [|14; 5; 8; 4|]; [|10; 12; 7; 9|]; [|15; 13; 11; 0|]|];
  i = 3; j = 0; h = 39}]

L'algorithme A* utilise une file de priorité q, que l'on va implémenter ici par arbre binaire de recherche (ABR), défini par le type :

type 'a abr = V | N of 'a * 'a abr * 'a abr

Chaque élément de l'ABR est un couple (priorité, élément) et l'arbre est ordonné par rapport à la priorité.

Écrire des fonctions add pour ajouter un élément à un ABR et extract_min pour extraire le minimum.

val add : ('a * 'b) abr -> 'a -> 'b -> ('a * 'b) abr
(* add a x y ajoute l'élément (x, y) à l'ABR a *)
val extract_min : 'a abr -> 'a * 'a abr
(* extract_min a renvoie le couple (x, b) où x est le minimum de a et b est l'arbre obtenu à partir de a en supprimant x *)

On rappelle le fonctionnement de l'algorithme $A^{\star}$ :

Dans notre situation, on en peut pas utiliser un tableau pour d car les sommets de $G$ sont ici des matrices (grilles).
On utilisera donc une table de hachage pour d dont chaque clé ('a) est un state et sa valeur ('b) est sa distance depuis l'état de départ :

Hashtbl.create : int -> ('a, 'b) Hashtbl.t crée une table vide. L'entier fourni donne la capacité initiale mais n'a que peu d'importance (la table sera redimensionnée au besoin).
Hashtbl.mem : ('a, 'b) Hashtbl.t -> 'a -> bool permet de tester si une clé est présente dans la table.
Hashtbl.add : ('a, 'b) Hashtbl.t -> 'a -> 'b -> unit ajoute une association à la table.
Hashtbl.replace : ('a, 'b) Hashtbl.t -> 'a -> 'b -> unit modifie une association existante, ou crée l'association si elle n'existait pas. On peut donc l'utiliser systématiquement à la place de Hashtbl.add.
Hashtbl.find : ('a, 'b) Hashtbl.t -> 'a -> 'b renvoie la valeur associée à une clé, ou lève l'exception Not_found si la valeur n'est pas dans la table.

Écrire une fonction a_star : state -> int qui prend en entrée un état initial et renvoie la longueur d'une solution trouvée par l'algorithme $A^*$ , en supposant qu'il en existe une. Tester avec les exemples suivants.

Exemples

(* état final *)
let final =
  let m = Array.make_matrix n n 0 in
  for i = 0 to n - 1 do
    for j = 0 to n - 1 do
      m.(i).(j) <- i * n + j
    done
  done;
  {grid = m; i = n - 1; j = n - 1; h = 0}

(* distance 5 de l'état final *)
let five =
  {grid = [|[|0; 15; 2; 3|]; [|4; 1; 5; 7|]; [|8; 9; 6; 11|]; [|12; 13; 10; 14|]|];
  i = 0; j = 1; h = -5}

(* distance 10 de l'état final *)
let ten =
  let moves = [U; U; L; L; U; R; D; D; L; L] in
  let state = copy final in
  List.iter (apply state) moves;
  state

a_star five;;
- : int = 5

a_star ten;;
- : int = 10

Graphe du taquin​

Algorithme A*​

Graphe du taquin

Algorithme A*